John Hilton Grace
| John Hilton Grace | |
|---|---|
| Born | 21 May 1873 Halewood, Lancashire |
| Died | 4 March 1958 (aged 84) |
| Nationality | British |
| Fields | Mathematics |
John Hilton Grace (21 May 1873 - 4 March 1958) was a British mathematician.
Contents |
Early life
He was born in Halewood, near Liverpool, the eldest of the six children of a farmer. He was educated at the village school and the Liverpool Institute. From there in 1892 he went up to Peterhouse College, Cambridge to study mathematics.[1]
Career
He was made a Fellow of Peterhouse in 1897 and became a Lecturer of Mathematics at Peterhouse and Pembroke colleges. An example of his work was his 1902 paper on the The Zeros of a Polynomial. In 1903 he collaborated with Alfred Young on their book Algebra of Invariants.[1]
He was elected a Fellow of the Royal Society in 1908.[1]
He spent 1916-1917 as Visiting Professor in Lahore and deputised for Professor MacDonald at Aberdeen University during the latter part of the war.[2]
In 1922 a breakdown in health forced his retirement from academic life and he spent the next part of his life in Norfolk.[1]
He died in Huntingdon in 1958 and was buried in the family grave at St. Nicholas Church, Halewood.
Theorem on zeros of a polynomial
If
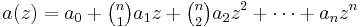 ,
,
are two polynomials that satisfy the apolarity condition, i.e. 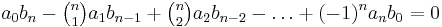 , then every neighborhood that includes all zeros of one polynomial also includes at least one zero of the other.[3][4]
, then every neighborhood that includes all zeros of one polynomial also includes at least one zero of the other.[3][4]
Corollary
Let 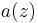 and
and 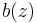 be defined as in the above theorem. If the zeros of both polynomials lie in the unit disk, then the zeros of the "composition" of the two,
be defined as in the above theorem. If the zeros of both polynomials lie in the unit disk, then the zeros of the "composition" of the two, 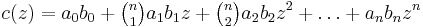 , also lie in the unit disk.[3]
, also lie in the unit disk.[3]
Publications
- Grace, J. H. (January 1936). "The actual irreducibility of some finite systems of invariant forms". Journal of the London Mathematical Society s1-11 (1): 20–21. doi:10.1112/jlms/s1-11.1.20. JFM 62.0075.02. Zbl 0013.14601. http://jlms.oxfordjournals.org/cgi/reprint/s1-11/1/20.
- Grace, J. H. (April 1930). "Two contract theorems". Journal of the London Mathematical Society s1-5 (2): 121–124. doi:10.1112/jlms/s1-5.2.121. http://jlms.oxfordjournals.org/cgi/reprint/s1-5/2/121.
- Grace, J. H. (January 1930). "The algebraic expression of projective properties". Journal of the London Mathematical Society s1-5 (1): 62–67. doi:10.1112/jlms/s1-5.1.62. http://jlms.oxfordjournals.org/cgi/reprint/s1-5/1/62.
- Grace, J. H. (1928). "Binary and ternary forms with prescribed polar systems". Proceedings of the London Mathematical Society s2-28 (1): 421–430. doi:10.1112/plms/s2-28.1.421. JFM 54.0133.03. http://plms.oxfordjournals.org/cgi/reprint/s2-28/1/421.
- Grace, J. H. (January 1928). "Surfaces related to a rational normal curve". Journal of the London Mathematical Society s1-3 (1): 34–38. doi:10.1112/jlms/s1-3.1.34. http://jlms.oxfordjournals.org/cgi/reprint/s1-3/1/34.
- Grace, J. H. (July 1927). "Note on ternary forms". Journal of the London Mathematical Society s1-2 (3): 182–185. doi:10.1112/jlms/s1-2.3.182. http://jlms.oxfordjournals.org/cgi/reprint/s1-2/3/182.
- Grace, J. H. (January 1927). "The four square theorem". Journal of the London Mathematical Society s1-2 (1): 3–8. doi:10.1112/jlms/s1-2.1.3. http://jlms.oxfordjournals.org/cgi/reprint/s1-2/1/3.
- Grace, J. H. (July 1926). "A point in enumerative geometry". Journal of the London Mathematical Society s1-1 (3): 167–170. doi:10.1112/jlms/s1-1.3.167. http://jlms.oxfordjournals.org/cgi/reprint/s1-1/3/167.
- Grace, J. H. (1918). "Note on a Diophantine approximation". Proceedings of the London Mathematical Society s2-17 (1): 316–319. doi:10.1112/plms/s2-17.1.316. http://plms.oxfordjournals.org/cgi/reprint/s2-17/1/316.
- Grace, J. H. (1918). "Tetrahedra in relation to spheres and quadrics". Proceedings of the London Mathematical Society s2-17 (1): 259–271. doi:10.1112/plms/s2-17.1.259. JFM 47.0612.01. http://plms.oxfordjournals.org/cgi/reprint/s2-17/1/259.
- Grace, J. H. (1918). "The classification of rational approximations". Proceedings of the London Mathematical Society s2-17 (1): 247–258. doi:10.1112/plms/s2-17.1.247. JFM 47.0166.01. http://plms.oxfordjournals.org/cgi/reprint/s2-17/1/247.
- Grace, J. H. (1904). "Note on the foregoing paper". Proceedings of the London Mathematical Society s2-1 (1): 208–209. doi:10.1112/plms/s2-1.1.208. http://plms.oxfordjournals.org/cgi/reprint/s2-1/1/208.
- Grace, J. H. (1904). "Extension of two theorems on covariants". Proceedings of the London Mathematical Society s2-1 (1): 151–153. doi:10.1112/plms/s2-1.1.151. JFM 34.0120.03. http://plms.oxfordjournals.org/cgi/reprint/s2-1/1/151.
- Grace, J. H.; A. Young (1903). The Algebra of Invariants. Cambridge University Press. http://books.google.com/?id=TrAAAAAAMAAJ.
- Grace, J. H.. "On the zeros of a polynomial". Proceedings of the Cambridge Philosophical Society 11: 352–357.
- Grace, J. H. (May 1902). "On perpetuants". Proceedings of the London Mathematical Society s1-35 (1): 319–331. doi:10.1112/plms/s1-35.1.319. http://plms.oxfordjournals.org/cgi/reprint/s1-35/1/319.
- Grace, J. H. (May 1902). "Types of perpetuants". Proceedings of the London Mathematical Society s1-35 (1): 107–114. doi:10.1112/plms/s1-35.1.107. http://plms.oxfordjournals.org/cgi/reprint/s1-35/1/107.
- Grace, J. H. (March 4, 1901). "A theorem on curves in a linear complex". Proceedings of the Cambridge Philosophical Society 11: 132–133. http://books.google.com/?id=IJ81AAAAIAAJ&pg=PA132.
- Grace, J. H. (March 1901). "Linear null systems of binary forms". Proceedings of the London Mathematical Society s1-34 (1): 168–172. doi:10.1112/plms/s1-34.1.168. JFM 33.0126.02. http://plms.oxfordjournals.org/cgi/reprint/s1-34/1/168.
- Grace, J. H. (November 1900). "On a class of plane curves". Proceedings of the London Mathematical Society s1-33 (1): 193–196. doi:10.1112/plms/s1-33.1.193. http://plms.oxfordjournals.org/cgi/reprint/s1-33/1/193.
- Grace, J. H. (1898). "Circles, spheres, and linear complexes". Transactions of the Cambridge Philosophical Society 16: 153–190.
References
- ^ a b c d Todd, J. A. (1958). "John Hilton Grace. 1873-1958". Biographical Memoirs of Fellows of the Royal Society 4: 92–97. doi:10.1098/rsbm.1958.0008.
- ^ Todd, J. A. (1959). "John Hilton Grace". Journal of the London Mathematical Society: 113–117. doi:10.1112/jlms/s1-34.1.113.
- ^ a b Szegő, Gábor (1922). "Bemerkungen zu einem Satz von J H Grace über die Wurzeln algebraischer Gleichungen". Mathematische Zeitschrift 13: 28–55. doi:10.1007/BF01485280. http://resolver.sub.uni-goettingen.de/purl?GDZPPN002366630. (German)
- ^ Rahman, Qazi I.; Gerhard Schmeisser (2002). "Grace's theorem and equivalent forms". Analytic Theory of Polynomials. Oxford University Press. pp. 107. ISBN 0198534930.
Further reading
- Hörmander, Lars (1954). "On a theorem of Grace". Mathematica Scandinavica 2: 55–64. http://resolver.sub.uni-goettingen.de/purl?GDZPPN002342987.
- Todd, John A. (November 1958). "John Hilton Grace". Biographical Memoirs of Fellows of the Royal Society 4: 92–97. doi:10.1098/rsbm.1958.0008. JSTOR 769502.
External links
- Works written by or about John Hilton Grace at Wikisource